引言

语言模型，在百度百科中的描述是：根据语言客观事实而进行的语言抽象数学建模，是一种对应关系。语言模型与语言客观事实之间的关系，如同数学上的抽象直线与具体直线之间的关系。在我看来，语言模型本质上其实是在解决这样一个问题：语句是否合理（更直白的说法就是，说的是不是人话 😏）。本文会介绍语言模型在计算机领域的几个转变的重要节点以及个人的一点小小的理解。

语言模型定义

标准定义：对于给定语言序列 $w_{1}, w_{2}, \ldots, w_{n}$，计算其概率大小，即 $P(w_{1}, w_{2}, \ldots, w_{n})$。

白话解释：给定一句话，判断其是不是正常的语句，或者说其作为正常语句出现的概率有多大。

统计语言模型

说到这里，就不得不谈谈 N 元文法模型（N-Gram Model）了。

N-Gram 模型基础

N-Gram 模型将语句（词序列）看作一个随机事件，并赋予其相应的概率来描述某语句出现的可能性。即，给定一个词汇集合 $V$，对于由 $V$ 中词汇组成的序列 $S=<w_{1}, w_{2}, \ldots, w_{n}>, w_{i} \in V$，N-Gram 模型将计算其出现的概率 $P(w_{1}^{n})$。

提前声明，为简化书写，我们使用符号 $w_{i}^{j}$ 来表示 $w_{i}, w_{i+1}, \ldots, w_{j}$。

首先，由链式法则（chain rule）得：
$$ P(w_{1}^{n})=P(w_{1})P(w_{2}|w_{1}) \cdots P(w_{n}|w_{1}^{n-1}) $$
然后，在统计语言模型中，我们会采用极大似然估计来计算每个词出现的条件概率（“统计语言模型”中的“统计”一词就体现在这儿）：
$$ \begin{aligned} P(w_{i}|w_{1}^{i-1})&=\frac{C(w_{1}^{i-1}, w_{i})}{\sum_w C(w_{1}^{i-1}, w)} \\ &=\frac{C(w_{1}^{i-1}, w_{i})}{C(w_{1}^{i-1})} \end{aligned} $$

其中，$C(\cdot)$ 表示子序列在训练集中出现的次数，即用频率近似概率。

显然，当序列较长时，这样直接进行计算是不现实的，原因有两点：

  • 参数空间过大：当序列过长时，$P(w_{n}|w_{1}^{n-1})$ 的可能性过多，难以估算
  • 数据过于稀疏：当序列过长时，很容易出现 $w_{1}^{n}$ 根本没在训练集中出现过的情况

因此，我们引入马尔可夫假设，即假设当前词的概率仅与前 $n-1$ 个词相关，得：

$$ P(w_{i}|w_{1}^{i-1}) \approx P(w_{i}|w_{i-n+1}^{i-1}) $$

基于上式，可以得到 N-Gram 模型的定义：

  • unigram：$n=1$，$P(w_{1}^{n}) \approx \prod_{i=1}^{n} P(w_{i})$
  • bigram：$n=2$，$P(w_{1}^{n}) \approx P(w_{1}) \prod_{i=2}^{n}P(w_{i}|w_{i-1})$
  • trigram：$n=3$，$P(w_{1}^{n}) \approx P(w_{1}) P(w_{2}|w_{1}) \prod_{i=1}^{n}P(w_{i}|w_{i-2}, w_{i-1})$
  • ……

需要注意的是，在进行实际操作时，有两个小 tricks。

其一，我们注意到在上述定义中，当 $n>1$ 时，会出现 $w_{i} (i \le 0)$ 的情况，此时可以通过在序列首添加一个或多个伪词（起始符，$\langle s \rangle$）来解决。譬如 $n=2$ 时，$P(w_{1}|\langle s \rangle)$。

其二，我们往往不会直接计算上述概率，而是采用对数概率，即 $\log (\prod_{i} p_{i}) = \sum_{i} \log p_{i}$

这样计算会有两大优势：

  • 将连乘转化为累加，加速计算
  • 防止数值溢出（概率本就是一些较小的数，连乘容易造成数值下溢）

起始标签/结束标签

为什么 N-Gram 需要开始标签/结束标签？

开门见山，先放结论：

$P(w_{1}^{n})$ 建模的 是 在无限长序列中出现子序列 $w_{1}^{n}$ 的概率，而 不是 序列 $w_{1}^{n}$ 出现的概率！

由于没有准确理解到这一点，导致一开始看 N-Gram 模型时对开始/结束标签的存在十分的困惑。

额外多说一句，上述理解仅代表个人的看法，我会在下面给出自己的解释，不一定正确，但以我目前的能力，只有这个解释能够说服我自己。（数学渣滓的悲哀）

这是很容易被初学者误解的一点，但只要理解了，会有豁然开朗的感觉。理由的话其实也很简单，我们回过头再仔细看看公式：$P(w_{1}^{n})=P(w_{1})P(w_{2}|w_{1}) \cdots P(w_{n}|w_{1}^{n-1})$，很容易发现，公式的第一项 $P(w_{1})$ 表示的是 $w_{1}$ 出现的概率，即 $w_{1}$ 在任何位置出现都被包含在内。这样就很清晰了，这里并没有限定 $w_{1}$ 前面还有多少词汇，当然了，也没有限定 $w_{n}$ 后面还有多少词汇，所以才说 $P(w_{1}^{n})$ 建模的是在无限长序列中所有出现子序列 $w_{1}^{n}$ 的总概率，如果用正则来表示的话大概就是 $(.\star?)w_{1}w_{2} \cdots w_{n}(.\star?)$ 吧。

这时候就体现出开始/结束标签的重要性了。在实践中，语句肯定只会是有限长的，像这种对无限长序列的建模其实毫无实际意义，但加上开始/结束标签就不一样了，界定了语句的开始与结束之后我们的模型就有能力建模任意长序列了（当然也包括无限长序列，只是由于概率的累乘，过长序列的出现概率几乎可以忽略不计，这也符合我们的直觉）。

下面举个栗子，为了简化说明过程，我们先考虑有开始标签而没有结束标签的情况。

假设我们有以下语料（是的，你没看错，就三句，词汇表 $V = (a, b, c)$）：

⟨s⟩ a b
⟨s⟩ a c
⟨s⟩ b a

取 $n=2$，即 bigram 模型，可得：

P(a|⟨s⟩) = 2/3
P(b|⟨s⟩) = 1/3
P(b|a) = 1/2
P(c|a) = 1/2
P(a|b) = 1

那么可以计算出结果如下：

P(ab) = 2/3 * 1/2 = 1/3
P(ac) = 2/3 * 1/2 = 1/3
P(ba) = 1/3 * 1 = 1/3
P(aa) = P(bb) = P(bc) = P(ca) = P(cb) = P(cc) = 0

桥豆麻袋！是不是有哪里不对？长度为 2 的序列概率和就等于 1 了，那其他长度的序列可咋办？但是考虑到我们前面说的就很容易理解了，这里其实应该是：

P(aa...) + P(ab...) + ... + P(cb...) + P(cc...) = 1

Bingo！那么现在加上结束标签再算一次：

⟨s⟩ a b ⟨/s⟩
⟨s⟩ a c ⟨/s⟩
⟨s⟩ b a ⟨/s⟩

各概率如下：

P(a|⟨s⟩) = 2/3
P(b|⟨s⟩) = 1/3
P(b|a) = 1/3
P(c|a) = 1/3
P(a|b) = 1/2
P(⟨/s⟩|a) = 1/3
P(⟨/s⟩|b) = 1/2
P(⟨/s⟩|c) = 1

计算结果如下：

P(ab) = 2/3 * 1/3 * 1/2 = 1/9
P(ac) = 2/3 * 1/3 * 1 = 2/9
P(ba) = 1/3 * 1/2 * 1/3 = 1/18
P(aa) = P(bb) = P(bc) = P(ca) = P(cb) = P(cc) = 0

P(aa) + P(ab) + ... + P(cb) + P(cc) = 7/18 < 1

可以再继续算算序列长度为 1 和 3 的概率。我们的语料分布情况使然，序列长度为 1~3 的概率和应该已经接近 1 了，这是合理的。

以上例子已经说明了为什么需要结束标签，反过来也是同样成立的。综上所述，要建模有限长序列，必须要有开始/结束标签的存在。

神经语言模型

有了 N-Gram 模型的基础，我们应该已经能够大致理解语言模型在做什么了。其实就是在给定一个词序列的前提下，预测该词序列的下一个词的概率情况，即 $P(w_{i}|w_{1}^{i-1})$，然后根据链式法则就可以计算出所有词序列出现的概率，即 $P(w_{1}^{n})$。N-Gram 模型中的 $n$ 的取值不同归根结底只是对 $P(w_{i}|w_{1}^{i-1})$ 的近似程度不同罢了。

基于前馈神经网络

既然我们已经理解了语言模型做的是在给定一个词序列的前提下预测该词序列的下一个词的概率情况，那么神经网络就想说话了，这事儿我熟啊。既然能用统计模型做，那么肯定也能用前馈神经网络来做。说到这里就不得不提到 Bengio 等人在 2001 年发表在 NIPS 上的论文 A Neural Probabilistic Language Model。

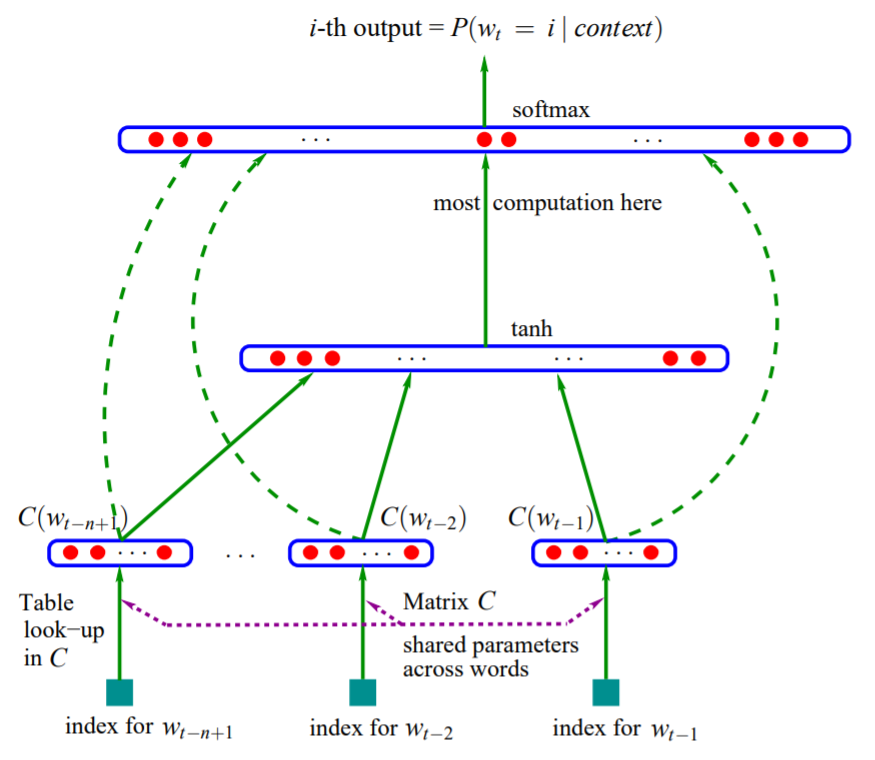
FFNN-LM.png

事实上这个神经网络模型也是一个 N-Gram 模型，即只考虑前 $n-1$ 个词的依赖关系，只不过是先将每个词都映射为连续空间中的一个词向量，再通过一个三层前馈神经网络去建模这种依赖关系（约束关系），相较于统计模型而言， 极大地增强了模型的泛化能力。模型公式如下（结合模型结构图很容易看懂了，不多 BB）：

$$ \begin{aligned} x &= concat(C(w)_{t-n+1}^{t-1}) \\ h &= tanh(Hx + d) \\ y &= Wx + Uh + b \end{aligned} $$

其中，$concat(\cdot)$ 为拼接函数，$C(w){i}^{j}$ 表示 $C(w{i}), \ldots, C(w_{j})$，$C(w_{i})$ 为 $w_{i}$ 的词向量。

基于递归神经网络

上面提到的前馈神经网络模型虽然很好地改善了统计模型泛化能力较差的问题，但是实质上还是基于 N-Gram 模型的思想，只考虑了有限的前文信息，那么在遇到长序列时候有没有什么办法能够考虑到足够远的前文信息呢？当然有！那就是 Mikolov 于 2010 年发表的论文 Recurrent neural network based language model 中提出的方法，该论文将 RNN 用在了 LM 训练任务上。公式如下（注意，这里的 RNN 指的是狭义上最基础的 RNN 网络，即只在 RNNCell 内部建立了权连接）：

$$ \begin{aligned} x_{t}^{i} &= concat(w_{t}^{i}, h_{t-1}^{i}) \\ h_{t}^{i} &= f(W^{i} x_{t}^{i} + b^{i}) \\ y_{t} &= g(U h_{t}^{n} + b) \end{aligned} $$

其中，输入的词嵌入 $w_{t}^{1}$ 使用最简单的 one-hot 编码，$n$ 为 RNN 网络层数，$i \in [1, n]$，$f(\cdot)$ 为 $sigmoid(\cdot)$，$g(\cdot)$ 为 $softmax(\cdot)$。

额外多说几句。单从理论上来说，RNN 应该是能够捕获足够远的前文信息的，但在实践中并非如此，一个合理的直觉是：因为 RNN 使用的这种最简单的 Cell 结构导致前文信息很容易随着时间步而逐渐被稀释，当遇到长序列时，较远的前文信息已经被稀释到几乎可以忽略不计了。也正因为如此，后来又进一步发展出了 LSTM 和 GRU 等各种衍生的递归神经网络（关于这部分，以后我会专门开一篇博客进行介绍）。

事实上，从统计语言模型开始一直到后面的各种递归神经网络，只要能够理解语言模型（Language Model）到底在做些什么，那么其他所有的东西也只是实现方法的不断改进优化罢了。

模型评价指标

（空）

To Be Continued.