引言

PyTorch 是一个开源的 Python 机器学习库，提供了两个高级功能：

  • 具有强大的 GPU 加速的张量计算
  • 包含自动求导系统的的深度神经网络（Autograd）

Autograd 包是 PyTorch 所有神经网络的核心，为张量上的所有操作提供自动求导机制。它是一个运行时定义的框架，即反向传播是随着对张量的操作来逐步决定的，这也意味着在每个迭代中都是可以不同的。

现在由于很多封装好的 API 的存在，导致我们在搭建自己的网络的时候并不需要过多地去关注求导这个问题，但如果能够对这个自动求导机制有所了解的话，对于我们写出更优雅更高效的代码无疑是帮助极大的。本文会简单介绍 PyTorch 的 Autograd 机制。

计算图

首先我们用一个简单的类比来了解一下什么是计算图：可以将计算图想象成一个复杂的管道结构，张量（数据）在其中通过特定的路径从入口向出口缓缓流动（这也就是 TensorFlow 中 Flow 的由来），每次张量从入口“流”到出口就表示完成了一次正向传播。在计算图中有两个最重要的元素：Tensor 和 Function，两者互相连接生成一个有向无环图（计算图），编码了完整的计算历史。

Tensor：n 维向量

张量 Tensor 可以理解为 n 维的向量，Tensor 是包中的核心类，通过将某个张量的属性 .requires_grad （默认为 False）设置为 True 可以追踪该张量上发生的所有操作，在完成计算之后可以通过 .backward() 反向传播来自动计算所有梯度（Gradient），并累加到 .grad 属性中。这就是 PyTorch 的自动求导。

$ x = torch.ones(2, 2, requires_grad=True); print(x)
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

Note：可以通过调用 .detach() 方法阻止一个张量被追踪，或者通过将代码块包裹在 with torch.no_grad(): 中，这点在评估模型时非常实用（因为在模型评估阶段并不需要进行梯度计算）。

Function：张量运算

在 PyTorch 的自动求导机制中，除了 Tensor 之外，还有另一个类 Function 也是非常重要的。

Function 指的是在计算图中对张量 Tensor 所进行的运算，譬如加减乘除卷积等。Function 内部有 .forward() 和 .backward() 两个方法，分别用于正向传播与反向传播。

我们的计算图在做正向传播的时候，除了 .forward() 本身的操作之外，还会自动为反向传播做准备，添加相应的 Function 节点，保存在张量的 .grad_fn 属性中。

$ y = x + 2; print(y)
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)

在计算图需要反向传播求梯度时只需调用 .backward() 即可。上例中，反向传播时需要做的操作就是 <AddBackward0>。

Gradient：方向导数

梯度：方向导数，即函数在该点处沿着该方向变化最快，变化率最大（梯度的模）。

一个实例

对自动求导机制有基本的了解之后可以来看一个简单的实例：

l1 = input x w1
l2 = l1 + w2
l3 = l1 x w3
l4 = l2 x l3
loss = mean(l4)

可以画出对应的计算图如下：

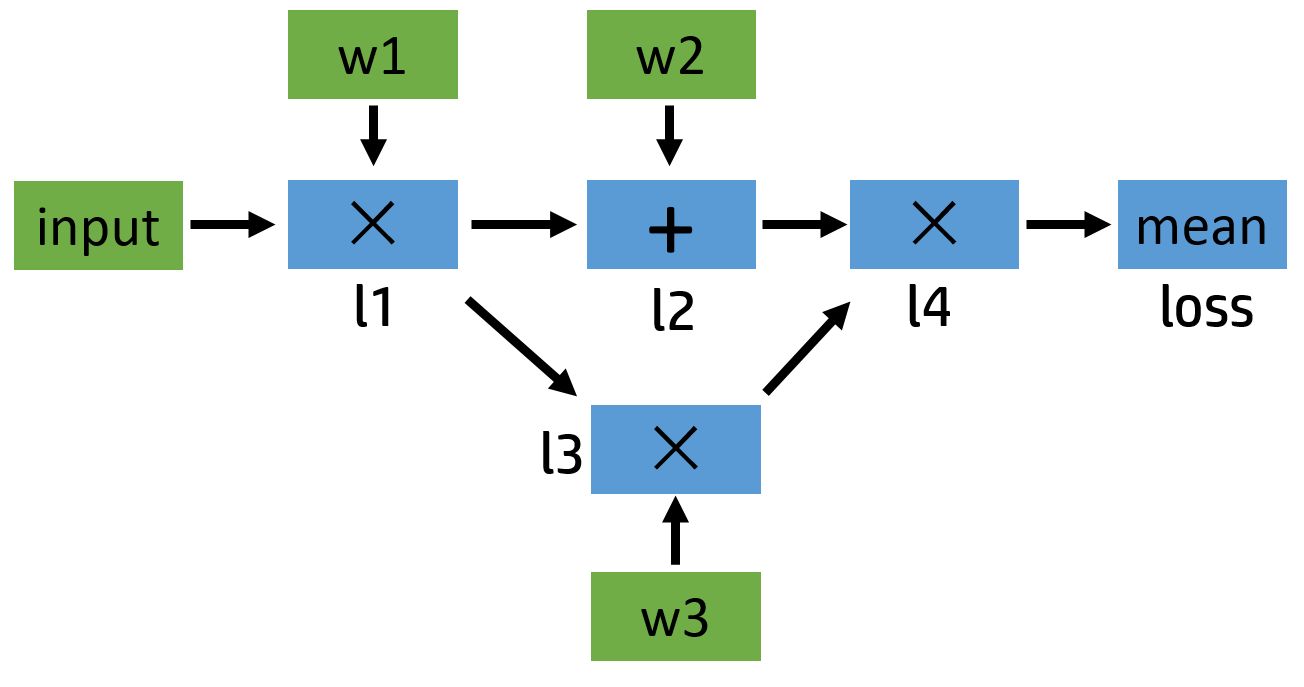
1781041624f4c9fb31df04d11dd6a84a.jpg

Note：其中 input 张量在实操时 .requires_grad 应设置为 False，并不需要进行追踪（因为在实操中 input 对应的是数据输入，并不是可训练参数，自然无需求导）。

手推结果：

in = [1., 1., 1., 1.]
w1 = [2., 2., 2., 2.]
w2 = [3., 3., 3., 3.]
w3 = [4., 4., 4., 4.]
l1 = in x w1 = [2., 2., 2., 2.]
l2 = l1 + w2 = [5., 5., 5., 5.]
l3 = l1 x w3 = [8., 8., 8., 8.]
l4 = l2 x l3 = [40., 40., 40., 40.]
ls = 40.

dls/dl4 = [0.25, 0.25, 0.25, 0.25]
dl4/dl3 = [5., 5., 5., 5.]
dl4/dl2 = [8., 8., 8., 8.]
dl3/dl1 = [4., 4., 4., 4.]
dl3/dw3 = [2., 2., 2., 2.]
dl2/dl1 = [1., 1., 1., 1.]
dl2/dw2 = [1., 1., 1., 1.]
dl1/dw1 = [1., 1., 1., 1.]

dls/dw3 = dls/dl4 * dl4/dl3 * dl3/dw3 = [2.5, 2.5, 2.5, 2.5]
dls/dw2 = dls/dl4 * dl4/dl2 * dl2/dw2 = [2.0, 2.0, 2.0, 2.0]
dls/dw1 = dls/dl4 * dl4/dl3 * dl3/dl1 * dl1/dw1
        + dls/dl4 * dl4/dl2 * dl2/dl1 * dl1/dw1
        = [7., 7., 7., 7.]

验证结果：

import torch

input = torch.ones([2, 2], requires_grad=False)
w1 = torch.tensor(2., requires_grad=True)
w2 = torch.tensor(3., requires_grad=True)
w3 = torch.tensor(4., requires_grad=True)

l1 = input * w1
l2 = l1 + w2
l3 = l1 * w3
l4 = l2 * l3
loss = l4.mean()

print(w1.data, w1.grad, w1.grad_fn)
print(l1.data, l1.grad, l1.grad_fn)
print(loss.data, loss.grad, loss.grad_fn)
# Out:
# tensor(2.)  None  None
# tensor([[2., 2.],
#         [2., 2.]])  None  <MulBackward0 object at 0x000001A9FC571E48>
# tensor(40.)  None  <MeanBackward0 object at 0x000001A9FC571E10>

loss.backward()

print(w1.grad, w2.grad, w3.grad)
print(l1.grad, l2.grad, l3.grad, l4.grad, loss.grad)
# Out:
# tensor(28.)  tensor(8.)  tensor(10.)
# None  None  None  None  None

这个例子中给定的参数 w 都只是常数，且涉及的运算都是加减乘除这类简单运算，但换成卷积之类的复杂运算之后原理仍然是一样的，只不过计算过程变得复杂了而已。

Note：可以看到 l1 ~ l4 的 .grad 都为 None，这其实是为了节省内存，所以默认并不会保存中间结果。可以通过调用 tensor.retain_grad() 来进行保存，或者通过调用 tensor.register_hook 来进行输出（并不保存）

l1.retain_grad()
l1.register_hook(lambda grad: print('l1 grad: ', grad))

参考资料

浅谈 PyTorch 中的 tensor 及使用

PyTorch 的 Autograd

PyTorch自动求导：Autograd

PyTorch 官方英文教程

PyTorch 官方英文文档